某学校游戏节活动中，设计了一个有奖转盘游戏，如图，A转盘被分成三个面积相等的扇形，B转盘被分成四个面积相等的扇形，每一个扇形都标有相应的数字，先转动A转盘，记下指针所指区域内的数字，再转动B转盘，记下指针所指区域内的数字（当指针在边界线上时，重新转动转盘，直到指针指向一个区域内为止）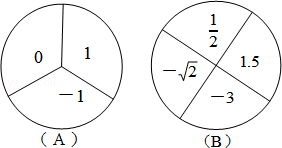
（1）请利用画树状图或列表的方法（只选其中一种），表示出转转盘可能出现的所有结果；
（2）如果将两次转转盘指针所指区域的数据相乘，乘积是无理数时获得一等奖，那么获得一等奖的概率是多少？
相关试题
对于数x、y，我们定义一种新的运算“⊕”：x⊕y=ax+by+c，其中a、b、c为常数，等式右边是通常的加法与乘法运算。已知3⊕5=15，4⊕7=28，那么求1⊕1的值。
小红和小新两人解方程组，
，
小红一边做作业，一边看电视，不小心把a给看错了，从而得到方程组的解为
，
小新一边做作业，一边吃零食，一走眼把b看错了，从而得到方程组的解为
，
若按正确的a、b计算，原方程组的解是什么？
和
的解相同，求a、b的值。
的解，并对这些方法进行比较。相关知识点
推荐套卷
粤公网安备 44130202000953号