某仓储系统有12条输入传送带，12条输出传送带．某日，控制室的电脑显示，每条输入传送带每小时进库的货物流量如图（1），每条输出传送带每小时出库的货物流量如图（2），而该日仓库中原有货物8吨，在0时至5时，仓库中货物存量变化情况如图（3）．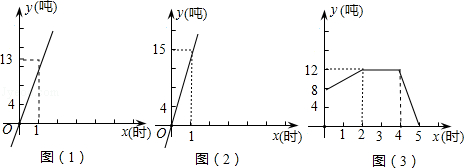
（1）每条输入传送带每小时进库的货物流量为多少吨？每条输出传送带每小时出库的货物流量为多少吨？
（2）在0时至5时内，仓库内货物存量y（吨）与时间x（小时）之间的函数关系式，并写出自变量x的取值范围；
（3）在4时至5时有多少条输入传送带和输出传送带在工作？
相关试题
，求代数式
的值．
已知:在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD. 探究下列问题:
（1）如图1，当点D与点C位于直线AB的两侧时，a=b=3，且∠ACB=60°，则CD=；
（2）如图2，当点D与点C位于直线AB的同侧时，a=b=6，且∠ACB=90°，则CD=；
（3）如图3，当∠ACB变化,且点D与点C位于直线AB的两侧时，求 CD的最大值及相应的∠ACB的度数.
图1图2图3
经过点E、G、H,现将
经过点F，得到抛物线
,求抛物线
相关知识点
推荐套卷
粤公网安备 44130202000953号