如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD,CE,若CE是⊙O的切线,解答下列问题: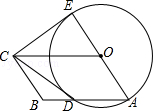
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.
相关知识点
推荐套卷
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.