（本小题满分10分）某同学对本地[30，55]岁的爱好阅读的人群随机抽取n人进行了一次调查，得到如下年龄统计表，其中不超过40岁的共有60人．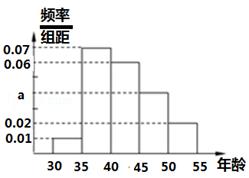
（Ⅰ）求出n，a的值；
（Ⅱ）从[45，55）岁年龄段爱好阅读的人中采用分层抽样法抽取6人，然后从这6人之中选2人为社区阅读大使，求选出的两人年龄均在[45，50）内的概率．
,
,
,求
取值范围; 
的最值，并给出最值时对应的x的值。
在(0,1]上是减函数。
.
为何实数，
总为增函数；
中, 
是
的中点
∥平面
；
∥平面
、
、
、
分别是正方体
的棱
、
、
、
的中点。
∥平面
；
∥平面
推荐套卷
（本小题满分10分）某同学对本地[30，55]岁的爱好阅读的人群随机抽取n人进行了一次调查，得到如下年龄统计表，其中不超过40岁的共有60人．
（Ⅰ）求出n，a的值；
（Ⅱ）从[45，55）岁年龄段爱好阅读的人中采用分层抽样法抽取6人，然后从这6人之中选2人为社区阅读大使，求选出的两人年龄均在[45，50）内的概率．
粤公网安备 44130202000953号