如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
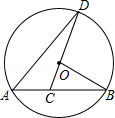
(1)弦长AB等于 (结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.
相关知识点
推荐套卷
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.

(1)弦长AB等于 (结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.