如图1,正方形ABCD中,E、F分别在AD、DG上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
(1)求证:∠ABE=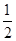 ∠BGE;
∠BGE;
(2)如图2,若AB=5,AE=2,求S△BEG;
(3)如图3,若E、F两点分别在AD、DC上运动,其它条件不变,试问:线段AE、EF、FC三者之间是否存在确定的数量关系?若存在,请写出它们之间的数量关系,并证明;若不存在,请说明理由.
相关知识点
推荐套卷
如图1,正方形ABCD中,E、F分别在AD、DG上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
(1)求证:∠ABE=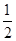 ∠BGE;
∠BGE;
(2)如图2,若AB=5,AE=2,求S△BEG;
(3)如图3,若E、F两点分别在AD、DC上运动,其它条件不变,试问:线段AE、EF、FC三者之间是否存在确定的数量关系?若存在,请写出它们之间的数量关系,并证明;若不存在,请说明理由.