在直角坐标系xOy中，以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C1的极坐标方程为ρ（sinθ+cosθ）=1，曲线C2的参数方程为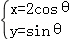
（θ为参数）．
（Ⅰ）求曲线C1的直角坐标方程与曲线C2的普通方程；
（Ⅱ）试判断曲线C1与C2是否存在两个交点？若存在，求出两交点间的距离；若不存在，说明理由．
相关试题
，使关于
的不等式
在
上的解集不是空集，设
的取值集合是
；若不等式
的解集为
，设实数
的取值集合是
，试求当
时，
的值域。
：
，
，
为极点，
为
，以
。
，
中，
，
，其中
＞0，对于函数
(n≥2)有
.
，
，
+
，求证：
＜b，证明：g(
＜（b﹣
（a，b为常数）且方程f(x)－x+12=0有两个实根为x1="3," x2=4.
.推荐套卷
在直角坐标系xOy中，以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C1的极坐标方程为ρ（sinθ+cosθ）=1，曲线C2的参数方程为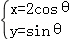（θ为参数）．
（Ⅰ）求曲线C1的直角坐标方程与曲线C2的普通方程；
（Ⅱ）试判断曲线C1与C2是否存在两个交点？若存在，求出两交点间的距离；若不存在，说明理由．
粤公网安备 44130202000953号