如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=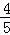 .
.
(1)求过A、C、D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A、E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.
相关知识点
推荐套卷
如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=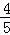 .
.
(1)求过A、C、D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A、E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.