(本小题满分l2分)
对于定义在区间D上的函数 ,若存在闭区间[a,b]
,若存在闭区间[a,b]  D和常数c,使得对任意x1
D和常数c,使得对任意x1 [a,b],都有
[a,b],都有 ,且对任意x2
,且对任意x2 D,当x2
D,当x2 [a,b]时
[a,b]时 恒成立,则称函数f(x)为区间D上的“平底型”函数
恒成立,则称函数f(x)为区间D上的“平底型”函数
(I)若函数 ="|mx-1|" +|x -2|是R上的“平底型”函数,求m的值;
="|mx-1|" +|x -2|是R上的“平底型”函数,求m的值;
(Ⅱ)判断函数 =x+|x-l|是否为R上的“平底型”函数?并说明理由;
=x+|x-l|是否为R上的“平底型”函数?并说明理由;
(Ⅲ)若函数g(x)="px+" |x –q|是区间[0,+∞)上的“平底型”函数,且函数的最小值为1,求p,q
的值.
相关知识点
推荐套卷
 的矩形板的四个角上截去四个相同的小正方形,作成一个无盖的盒子,求盒子容积的最大值。
的矩形板的四个角上截去四个相同的小正方形,作成一个无盖的盒子,求盒子容积的最大值。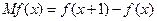 为函数
为函数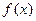 的边际函数,某企业每月最多生产
的边际函数,某企业每月最多生产 台报警器,已知每生产
台报警器,已知每生产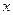 台的收入函数为
台的收入函数为 (单位:元),其成本函数为
(单位:元),其成本函数为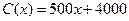 (单位:元),利润是收入与成本的差。(1)求利润函数
(单位:元),利润是收入与成本的差。(1)求利润函数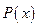 及其边际函数
及其边际函数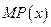 ;(2)利润函数
;(2)利润函数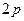 ,问绕这个三角形的底边旋转一周所成的几何体的体积最大时,各边长分别是多少?
,问绕这个三角形的底边旋转一周所成的几何体的体积最大时,各边长分别是多少?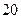 元购进一批商品,若该商品零售价定为
元购进一批商品,若该商品零售价定为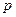 元,则销售量
元,则销售量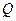 (单位:件)与零售价
(单位:件)与零售价 ,问该商品零售价定为多少时利润
,问该商品零售价定为多少时利润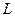 最大,并求出最大利润。(利润=销售收入
最大,并求出最大利润。(利润=销售收入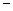 进货支出)
进货支出)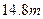 1的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长
1的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长 ,那么高为多少时容器的容积最大?并求出它的最大容积。
,那么高为多少时容器的容积最大?并求出它的最大容积。 粤公网安备 44130202000953号
粤公网安备 44130202000953号