(本小题满分13分)
设关于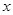 的一元二次方程
的一元二次方程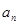
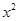
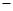
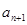
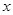
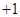
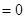 (
(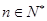 )有两根
)有两根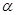 和
和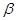 ,且满足
,且满足
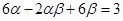 .
.
(Ⅰ)试用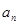 表示
表示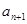 ;
;
(Ⅱ)求证:数列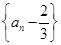 是等比数列;
是等比数列;
(Ⅲ)当 时,求数列
时,求数列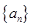 的通项公式,并求数列
的通项公式,并求数列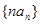 的前
的前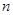 项和
项和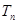 .
.
相关知识点
推荐套卷
(本小题满分13分)
设关于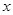 的一元二次方程
的一元二次方程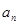
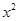
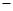
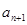
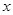
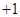
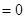 (
(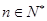 )有两根
)有两根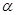 和
和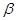 ,且满足
,且满足
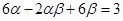 .
.
(Ⅰ)试用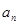 表示
表示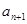 ;
;
(Ⅱ)求证:数列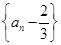 是等比数列;
是等比数列;
(Ⅲ)当 时,求数列
时,求数列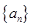 的通项公式,并求数列
的通项公式,并求数列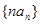 的前
的前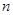 项和
项和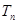 .
.