某同学用“五点法”画函数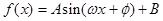 (
( )在某一个周期内的图象时,列表并填入的部分数据如下表:
)在某一个周期内的图象时,列表并填入的部分数据如下表:
 |
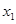 |
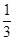 |
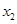 |
 |
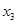 |
 |
 |
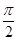 |
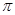 |
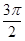 |
 |
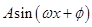 |
 |
 |
 |
 |
 |
(Ⅰ)请求出上表中的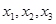 ,并直接写出函数
,并直接写出函数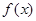 的解析式;
的解析式;
(Ⅱ)将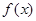 的图象沿x轴向右平移
的图象沿x轴向右平移 个单位得到函数
个单位得到函数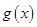 ,若函数
,若函数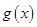 在
在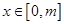 (其中
(其中 上的值域为
上的值域为 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为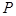 、
、 ,求
,求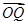 与
与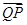 夹角θ的大小.
夹角θ的大小.
相关知识点
推荐套卷
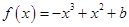 ,
,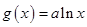 .
.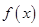 在
在 上的最大值为
上的最大值为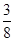 ,求实数
,求实数 的值;
的值;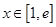 ,都有
,都有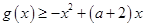 恒成立,求实数
恒成立,求实数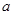 的取值范围;
的取值范围;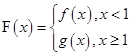 ,对任意给定的正实数
,对任意给定的正实数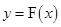 上是否存在两点
上是否存在两点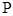 、
、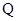 ,使得
,使得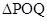 是以
是以 (
(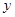 轴上?请说明理由.
轴上?请说明理由. 中,
中,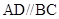 ,
, ,
, 平面
平面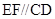 ,
,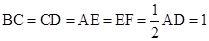 .
. 平面
平面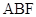 ;
;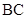 上是否存在点
上是否存在点 ,使二面角
,使二面角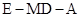 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,说明理由.
的长;若不存在,说明理由.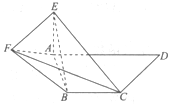
 的公差为
的公差为 ,前
,前 项和为
项和为 ,且
,且 .
. 与前
与前 的前三项,记数列
的前三项,记数列 的前
的前 ,若存在
,若存在 ,使得对任意
,使得对任意 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 的底面是菱形,
的底面是菱形, ,
, ,
, ,
,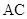 与
与 交于
交于 点,
点,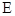 ,
,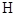 分别为
分别为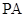 ,
,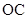 的中点.
的中点.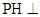 平面
平面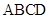 ;
;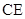 与平面
与平面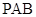 所成角的正弦值.
所成角的正弦值.
 中,角
中,角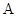 ,
, ,
, 所对的边为
所对的边为 ,
,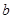 ,
, ,且满足
,且满足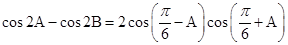 .
. 且
且 ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号