如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．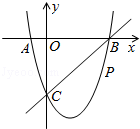
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．
有A、B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字
，
和
．小明从
布袋中随机取出一个小球，记录其标有的数字为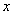
，再从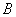
布袋中随机取出一个小球，记录其标有的数字为
，这样就确定点
的一个坐标为
．用列表或画树状图的方法写出点
的所有可能坐标；求点
落在直线
上的概率
探究
在图1中，已知线段AB，CD，其中点分别为E，F．
①若A (-1，0)， B (3，0)，则E点坐标为__________；
②若C (-2，2)， D (-2，-1)，则F点坐标为__________；
归纳
①在图2中，已知线段AB的端点坐标为A(1，1) ，B(3，3)，
则AB 的中点C的坐标__________
②无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为
A(a，b)，B(c，d)， AB中点C的坐标为______ 
运用
在图3中，一次函数
与反比例函数
的图象交点为A（-1，-3），B（3 , n）．
①求出m、n的值；
②求出一次函数的表达式；
③若四边形AOBP为平行四边形,请利用上面的结论求出顶点P的坐标．
公司经营甲、乙两种商品，每件甲种商品进价12万元，售价14．5万元；每件乙种商品进价8万元，售价lO万元，且它们的进价和售价始终不变．现准备购进甲、乙两种商品共20件，所用资金不低于190万元，不高于200万元．该公司有哪几种进货方案?
该公司采用哪种进货方案可获得最大利润?最大利润是多少?
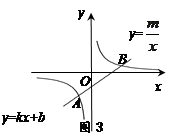
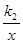只有—个交点A(1，2)，且与x轴、y轴分别交于B,C 两点，AD垂直平分OB，垂足为D，求直线、双曲线的解析式．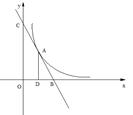
粤公网安备 44130202000953号