（本小题满分12分）（如图，某海滨浴场的岸边可近似地看成直线，位于岸边A处的救生员发现海中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D处，然后游向B处，若救生员在岸边的行进速度为6米/秒，在海中的行进速度为2米/秒，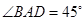
。
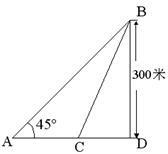
（1）分析救生员的选择是否正确；
（2）在AD上找一点C，使救生员从A到B的时间为最短，并求出最短时间。
相关试题
满足方程
的最大值与最小值
为参数，圆C：
上,且被直线y=x截得的弦长为
，求圆C的方程．
．求动点M的轨迹方程，并说明它表示什么曲线．
推荐套卷
（本小题满分12分）（如图，某海滨浴场的岸边可近似地看成直线，位于岸边A处的救生员发现海中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D处，然后游向B处，若救生员在岸边的行进速度为6米/秒，在海中的行进速度为2米/秒，。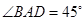
（1）分析救生员的选择是否正确；
（2）在AD上找一点C，使救生员从A到B的时间为最短，并求出最短时间。
粤公网安备 44130202000953号