如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴,如果A点坐标是(﹣1,2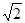 ),C点坐标是(3,﹣2
),C点坐标是(3,﹣2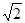 ).
).

(1)直接写出B点和D点的坐标B( );D( ).
(2)将这个长方形先向右平移1个单位长度长度,再向下平移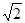 个单位长度,得到长方形A1B1C1D1,请你写出平移后四个顶点的坐标;
个单位长度,得到长方形A1B1C1D1,请你写出平移后四个顶点的坐标;
(3)如果Q点以每秒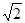 个单位长度的速度在长方形ABCD的边上从A出到到C点停止,沿着A﹣D﹣C的路径运动,那么当Q点的运动时间分别是1秒,4秒时,△BCQ的面积各是多少?请你分别求出来.
个单位长度的速度在长方形ABCD的边上从A出到到C点停止,沿着A﹣D﹣C的路径运动,那么当Q点的运动时间分别是1秒,4秒时,△BCQ的面积各是多少?请你分别求出来.
相关知识点
推荐套卷

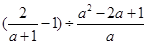 ,在-1,1,0,2四个数中选一个你喜欢的数,代入求值。
,在-1,1,0,2四个数中选一个你喜欢的数,代入求值。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号