某中学组织学生开展课外阅读活动，为了解本校学生每周课外阅读的时间量t（小时），采用随机抽样的方法抽取部分学生进行了问卷调查，调查结果按0≤t＜2，2≤t＜3，3≤t＜4，t≥4分为四个等级，并分别用A、B、C、D表示，根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：
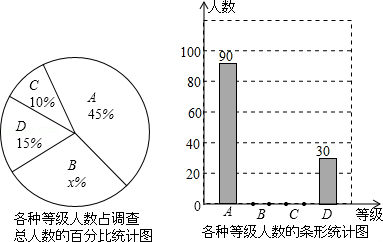
（1）本次随机抽取的学生人数为 人；
（2）求出x值，并将不完整的条形统计图补充完整；
（3）若该校共有学生2500人，试估计每周课外阅读量满足2≤t＜4的人数．
相关试题
，求代数式
的
值．
中，
，
于
，点
在线段
上，
，
在线段
上，请你从以下两个条件中选择一个作为条件，证明△
≌△
．
∥
； （2）
．
并把解集在数轴上表示出来．已知：抛物线
经过坐标原点．
（1）求抛物线的解析式和顶点B的坐标；
（2）设点A是抛物线与
轴的另
一个交点，试在
轴上确定一点P，使PA+PB最短，并求出点P的坐标；
（3）过
点A作AC∥BP
交轴于点C，求到直线AP、AC、CP距离相等的点的坐标．
，
上任意两点，C是直线
AB (k≠0).
时，在图（1）中，作∠BEF＝∠ABC，EF交直线相关知识点
推荐套卷
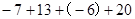
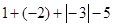
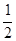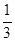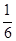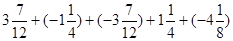
粤公网安备 44130202000953号