（1）如图1，已知△ABC中，∠BAC=45°，AB=AC，AD⊥BC于D，将△ABC沿AD剪开，并分别以AB、AC为轴翻转，点E、F分别是点D的对应点，得到△ABE和△ACF （与△ABC在同一平面内）．延长EB、FC相交于G点，证明四边形AEGF是正方形；
（2）如果（1）中AB≠AC，其他不变，如图2．那么四边形AEGF是否是正方形？请说明理由；
（3）在（2）中，若BD=2，DC=3，求AD的长．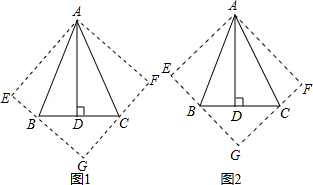
相关试题
如图，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）．
（1）画出△ABC，关于原点对称的三角形△A′B′C′；
（2）将三角形A、B、C绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点的坐标；
（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
，其中a=
，b=-3．
如图，矩形OABC摆放在平面直角坐标系xOy中，点A在x轴上，点C在y轴上，OA=3，OC=2，P是BC边上一点且不与B重合，连结AP，过点P作∠CPD=∠APB，交x轴于点D，交y轴于点E，过点E作EF∥AP交x轴于点F．
（1）若△APD为等腰直角三角形，求点P的坐标；
（2）若以A，P，E，F为顶点的四边形是平行四边形，求直线PE的解析式．
相关知识点
推荐套卷
粤公网安备 44130202000953号