(本小题满分13分)如图,已知菱形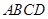 的边长为
的边长为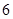 ,
,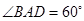 ,
,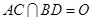 .将菱形
.将菱形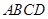 沿对角线
沿对角线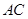 折起,使
折起,使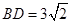 ,得到三棱锥
,得到三棱锥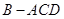 .
.
(Ⅰ)若点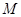 是棱
是棱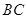 的中点,求证:
的中点,求证: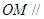 平面
平面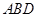 ;
;
(Ⅱ)求二面角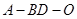 的余弦值;
的余弦值;
(Ⅲ)设点 是线段
是线段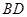 上一个动点,试确定
上一个动点,试确定 点的位置,使得
点的位置,使得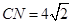 ,并证明你的结论.
,并证明你的结论.
推荐套卷
(本小题满分13分)如图,已知菱形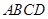 的边长为
的边长为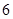 ,
,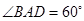 ,
,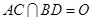 .将菱形
.将菱形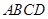 沿对角线
沿对角线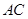 折起,使
折起,使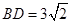 ,得到三棱锥
,得到三棱锥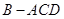 .
.
(Ⅰ)若点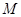 是棱
是棱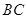 的中点,求证:
的中点,求证: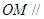 平面
平面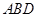 ;
;
(Ⅱ)求二面角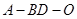 的余弦值;
的余弦值;
(Ⅲ)设点 是线段
是线段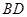 上一个动点,试确定
上一个动点,试确定 点的位置,使得
点的位置,使得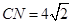 ,并证明你的结论.
,并证明你的结论.