设单调递增函数
的定义域为
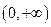，且对任意的正实数x,y有：
且
．
⑴．一个各项均为正数的数列
满足:
其中
为数列的前n项和,求数列的通项公式；
⑵．在⑴的条件下，是否存在正数M使下列不等式：
对一切
成立？若存在，求出M的取值范围；若不存在，请说明理由．
，解不等式
；
时，若
，使得不等式
成立，求实数
的取值范围．
，解不等式
；
有最小值，求实数
的取值范围.
(
)．
的单调区间；
（
）的单调性证明：当
时，
；
,且
均为正实数, 
时，
．
满足
，求证：
．
.推荐套卷
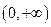设单调递增函数的定义域为，且对任意的正实数x,y有：且．
⑴．一个各项均为正数的数列满足:其中为数列的前n项和,求数列的通项公式；
⑵．在⑴的条件下，是否存在正数M使下列不等式：
对一切成立？若存在，求出M的取值范围；若不存在，请说明理由．
粤公网安备 44130202000953号