已知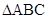 中,角
中,角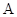 ,
,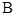 ,
,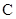 所对的边分别为
所对的边分别为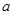 ,
,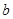 ,
,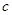 ,若
,若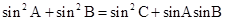 ,
,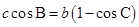 .
.
(1)判断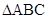 的形状;
的形状;
(2)在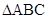 的边
的边 ,
,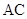 上分别取
上分别取 ,
, 两点,使沿线段
两点,使沿线段 折叠三角形时,顶点
折叠三角形时,顶点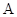 正好落在边
正好落在边 上的
上的 点处,设
点处,设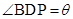 ,当
,当 最小时,求
最小时,求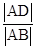 的值.
的值.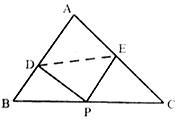
相关知识点
推荐套卷
已知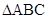 中,角
中,角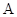 ,
,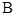 ,
,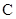 所对的边分别为
所对的边分别为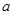 ,
,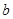 ,
,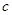 ,若
,若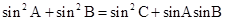 ,
,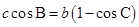 .
.
(1)判断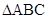 的形状;
的形状;
(2)在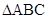 的边
的边 ,
,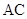 上分别取
上分别取 ,
, 两点,使沿线段
两点,使沿线段 折叠三角形时,顶点
折叠三角形时,顶点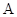 正好落在边
正好落在边 上的
上的 点处,设
点处,设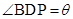 ,当
,当 最小时,求
最小时,求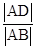 的值.
的值.