已知直线l的参数方程为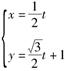 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 为参数).
为参数).
(I )已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II )设点Q是曲线C上的一个动点,求点Q到直线l的距离的最小值与最大值.
推荐套卷
已知直线l的参数方程为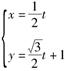 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 为参数).
为参数).
(I )已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II )设点Q是曲线C上的一个动点,求点Q到直线l的距离的最小值与最大值.