如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
相关知识点
推荐套卷
 只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,
只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,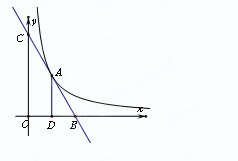

 倍,问乘公交车平均速度?
倍,问乘公交车平均速度?
 粤公网安备 44130202000953号
粤公网安备 44130202000953号