为了弘扬“社会主义核心价值观”，市政府在广场树立公益广告牌，如图所示，为固定广告牌，在两侧加固钢缆，已知钢缆底端D距广告牌立柱距离CD为3米，从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°．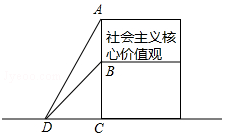
（1）求公益广告牌的高度AB；
（2）求加固钢缆AD和BD的长．（注意：本题中的计算过程和结果均保留根号）
的对角线
和
相交于点
，
,试判断四边形
的形状，并说明理由．
相关知识点
推荐套卷
为了弘扬“社会主义核心价值观”，市政府在广场树立公益广告牌，如图所示，为固定广告牌，在两侧加固钢缆，已知钢缆底端D距广告牌立柱距离CD为3米，从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°．
（1）求公益广告牌的高度AB；
（2）求加固钢缆AD和BD的长．（注意：本题中的计算过程和结果均保留根号）
粤公网安备 44130202000953号