如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（﹣1，5），B（﹣4，1），C（﹣1，1）将△ABC绕点A逆时针旋转90°，得到△AB′C′，点B，C的对应点分别为点B′，C′，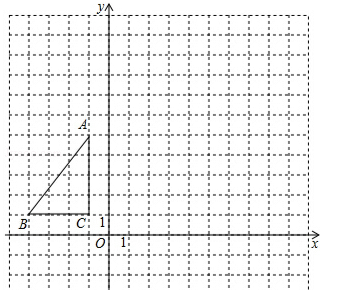
（1）画出△AB′C′；
（2）写出点B′，C′的坐标；
（3）求出在△ABC旋转的过程中，点C经过的路径长．
相关试题
的值。相关知识点
推荐套卷
如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（﹣1，5），B（﹣4，1），C（﹣1，1）将△ABC绕点A逆时针旋转90°，得到△AB′C′，点B，C的对应点分别为点B′，C′，
（1）画出△AB′C′；
（2）写出点B′，C′的坐标；
（3）求出在△ABC旋转的过程中，点C经过的路径长．
粤公网安备 44130202000953号