1、探究
(1) 在图1中,已知线段AB,CD.
①若A (-1,0), B (3,0),则AB=__________;
②若C (-2,2), D (-2,-1),则CD=__________;
(2)在图2中,已知线段AB的端点坐标为A(1,1) ,B(4,3),请求出图中线段AB的长度.
2、归纳
无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d),请用a、b、c、d表示线段AB的长度(不必证明)。
相关知识点
推荐套卷
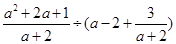 ,然后从﹣2,﹣1,1,2四个数中选择一个合适的数作为a的值代入求值.
,然后从﹣2,﹣1,1,2四个数中选择一个合适的数作为a的值代入求值.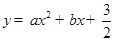 (
(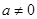 )经过点A(﹣1,0)和B(3,0).
)经过点A(﹣1,0)和B(3,0).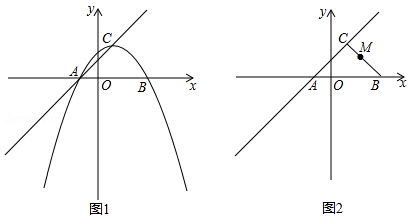
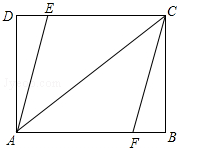
 .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
 ,求图中阴影部分的面积;
,求图中阴影部分的面积; ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.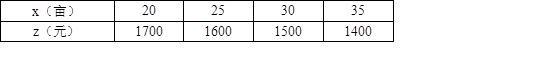
 粤公网安备 44130202000953号
粤公网安备 44130202000953号