已知:如图,直线y=﹣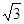 x+4
x+4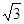 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=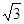 x交于点P.
x交于点P.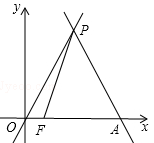
(1)求点P的坐标.
(2)动点F从原点O出发,以每秒1个单位的速度在线段OA上向点A作匀速运动,连接PF,设运动时间为t秒,△PFA的面积为S,求出S关于t的函数关系式.
(3)若点M是y轴上任意一点,点N是坐标平面内任意一点,若以O、M、N、P为顶点的四边形是平行四边形,请直接写出点N的坐标.
相关知识点
推荐套卷
已知:如图,直线y=﹣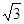 x+4
x+4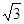 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=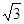 x交于点P.
x交于点P.
(1)求点P的坐标.
(2)动点F从原点O出发,以每秒1个单位的速度在线段OA上向点A作匀速运动,连接PF,设运动时间为t秒,△PFA的面积为S,求出S关于t的函数关系式.
(3)若点M是y轴上任意一点,点N是坐标平面内任意一点,若以O、M、N、P为顶点的四边形是平行四边形,请直接写出点N的坐标.