某商场在今年“十一”黄金周期间采取购物抽奖的方式促销(每人至多抽奖一次),设了金奖和银奖,奖券共2000张。在某一时段对30名顾客进行调查,其中有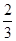 的顾客没有得奖,而得奖的顾客中有
的顾客没有得奖,而得奖的顾客中有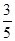 的顾客得银奖,若对这30名顾客随机采访3名顾客。
的顾客得银奖,若对这30名顾客随机采访3名顾客。
(1)求选取的3名顾客中至少有一人得金奖的概率;
(2)求选取的3名顾客中得金奖人数不多于得银奖人数的概率。
推荐套卷
某商场在今年“十一”黄金周期间采取购物抽奖的方式促销(每人至多抽奖一次),设了金奖和银奖,奖券共2000张。在某一时段对30名顾客进行调查,其中有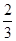 的顾客没有得奖,而得奖的顾客中有
的顾客没有得奖,而得奖的顾客中有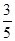 的顾客得银奖,若对这30名顾客随机采访3名顾客。
的顾客得银奖,若对这30名顾客随机采访3名顾客。
(1)求选取的3名顾客中至少有一人得金奖的概率;
(2)求选取的3名顾客中得金奖人数不多于得银奖人数的概率。