施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系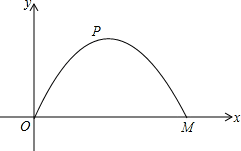
(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明.
相关知识点
推荐套卷
施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系
(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明.