如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．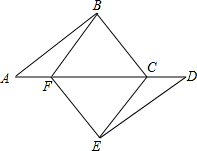
（1）求证：四边形BCEF是平行四边形，
（2）若∠ABC=90°，AB=4，BC=3，当AF为何值时，四边形BCEF是菱形．
相关试题
x2y)＋x2y2]，其中
；（2）解方程：
，4，0，-1.5，5，
，-
.把上述各数填在相应的集合里：
相关知识点
推荐套卷
如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．
（1）求证：四边形BCEF是平行四边形，
（2）若∠ABC=90°，AB=4，BC=3，当AF为何值时，四边形BCEF是菱形．
粤公网安备 44130202000953号