某校师生积极为灾区捐款捐物,在得知灾区急需帐篷后,学校采购了两种规格的帐篷;可供3人居住的小帐篷,每顶价格150元,可供10人居住的大帐篷,每顶价格400元.学校花去捐款75000元采购这两种帐篷,正好可供1800人居住.
(1)学校分别采购了多少顶小帐篷和大帐篷?
(2)学校准备租用甲,乙两种运输车共12辆把帐篷运往灾区,已知甲型运输车每辆可同时运15小帐篷8顶大帐篷,乙型运输车可同时运6顶小帐篷16顶大帐篷,学校应该如何安排甲、乙两种型号的运输车可一次性将这批帐篷运往灾区?
相关知识点
推荐套卷
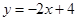 的图像,并求函数图像与两坐标轴所围成的三角形面积.
的图像,并求函数图像与两坐标轴所围成的三角形面积.
 的多项式
的多项式 不含三次项,求
不含三次项,求 的值.
的值.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号