为响应国家要求中小学生每天锻炼 小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图
小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图 和图
和图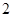 .问:
.问:
(1)该班共有多少名学生?若全年级共有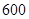 名学生,估计全年级参加兵乓球活动的学生有多少名?
名学生,估计全年级参加兵乓球活动的学生有多少名?
(2)请在图 将“兵乓球”部分的图形补充完整,并求出扇形统计图,表示“足球”的扇形圆心角的度数
将“兵乓球”部分的图形补充完整,并求出扇形统计图,表示“足球”的扇形圆心角的度数
相关知识点
推荐套卷
为响应国家要求中小学生每天锻炼 小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图
小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图 和图
和图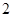 .问:
.问:
(1)该班共有多少名学生?若全年级共有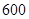 名学生,估计全年级参加兵乓球活动的学生有多少名?
名学生,估计全年级参加兵乓球活动的学生有多少名?
(2)请在图 将“兵乓球”部分的图形补充完整,并求出扇形统计图,表示“足球”的扇形圆心角的度数
将“兵乓球”部分的图形补充完整,并求出扇形统计图,表示“足球”的扇形圆心角的度数