抛物线 与x轴交于A,B两点(OA<OB),与y轴交于点C.
与x轴交于A,B两点(OA<OB),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<2).
①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时, 的值最小,求出这个最小值并写出此时点E,P的坐标;
的值最小,求出这个最小值并写出此时点E,P的坐标;
②在满足①的条件下,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
 12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000
12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000 和乙种板材12000
和乙种板材12000 两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间 型板房和一间
型板房和一间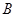 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示: ,
,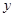 的方程组
的方程组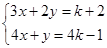 的解
的解 ,求
,求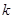 的取值范围.
的取值范围.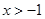 ;⑵
;⑵ ;⑶
;⑶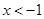 ;⑷
;⑷ ;⑸
;⑸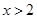 且
且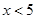


 粤公网安备 44130202000953号
粤公网安备 44130202000953号