如图，▱ABCD中，点E，F在直线AC上（点E在F左侧），BE∥DF．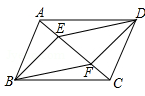
（1）求证：四边形BEDF是平行四边形；
（2）若AB⊥AC，AB=4，BC=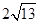
，当四边形BEDF为矩形时，求线段AE的长．
相关知识点
推荐套卷
如图，▱ABCD中，点E，F在直线AC上（点E在F左侧），BE∥DF．
（1）求证：四边形BEDF是平行四边形；
（2）若AB⊥AC，AB=4，BC=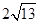，当四边形BEDF为矩形时，求线段AE的长．
粤公网安备 44130202000953号