如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．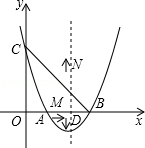
（1）求二次函数的表达式；
（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；
（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．
相关试题
已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，
（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．
在平面直角坐标系中，矩形ABCD的边AB在x轴上，点A、B的横坐标分别为a+2与2a﹣5，且关于y轴对称，BC的长为3，且点C在第三象限．
（1）求顶点A、C的坐标；
（2）若y=kx+b是经过点B，且与AC平行的一条直线，试确定它的解析式．
相关知识点
推荐套卷
粤公网安备 44130202000953号