(本小题满分13分)已知函数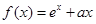 ,
,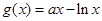 ,其中
,其中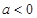 ,
,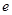 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求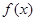 在
在 上的最小值;
上的最小值;
(Ⅱ)试探究能否存在区间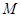 ,使得
,使得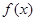 和
和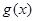 在区间
在区间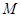 上具有相同的单调性?若能存在,说明区间
上具有相同的单调性?若能存在,说明区间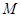 的特点,并指出
的特点,并指出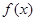 和
和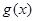 在区间
在区间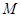 上的单调性;若不能存在,请说明理由.
上的单调性;若不能存在,请说明理由.
推荐套卷
(本小题满分13分)已知函数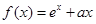 ,
,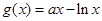 ,其中
,其中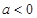 ,
,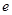 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求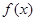 在
在 上的最小值;
上的最小值;
(Ⅱ)试探究能否存在区间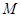 ,使得
,使得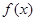 和
和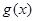 在区间
在区间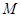 上具有相同的单调性?若能存在,说明区间
上具有相同的单调性?若能存在,说明区间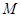 的特点,并指出
的特点,并指出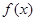 和
和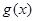 在区间
在区间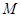 上的单调性;若不能存在,请说明理由.
上的单调性;若不能存在,请说明理由.