（本题6分）如图，△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上，将△ABC向右平移3格，再向上平移2格．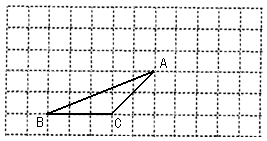
（1）请在图中画出平移后的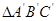
；
（2）△ABC的面积为 _；
（3）若AB的长约为5．4，求出AB边上的高（结果保留整数）．
．
，
，
……根据你发现的规律，计算：
+
+
+……+
，
+
+
+……+
(n为正整数)
，求
的值．
，其中
．相关知识点
推荐套卷
（本题6分）如图，△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上，将△ABC向右平移3格，再向上平移2格．
（1）请在图中画出平移后的；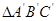
（2）△ABC的面积为 _；
（3）若AB的长约为5．4，求出AB边上的高（结果保留整数）．
粤公网安备 44130202000953号