已知函数 ,其中常数
,其中常数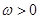 .
.
(1)令 ,判断函数
,判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)令 将函数
将函数 向左平移
向左平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图像.对任意
的图像.对任意 ,求
,求 在区间
在区间 上的零点 个数的所有可能值.
上的零点 个数的所有可能值.
相关知识点
推荐套卷
已知函数 ,其中常数
,其中常数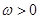 .
.
(1)令 ,判断函数
,判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)令 将函数
将函数 向左平移
向左平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图像.对任意
的图像.对任意 ,求
,求 在区间
在区间 上的零点 个数的所有可能值.
上的零点 个数的所有可能值.