（本小题满分10分）选修4-1：几何证明选讲
已知AB是⊙O的直径，F为圆上一点，∠BAF的角平分线与圆交于点C过点C作圆的切线与直线
相交于点D，若AB＝6，∠DAB＝
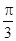
（1）证明：AD⊥CD；
（2）求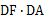
的值及四边形ABCD的面积．
相关试题
, 计算:
; (2) 
；（2）
的图像都过点P（2，0），且在点P处有相同的切线。
的最小值。
（e为自然对数的底数）。
的最小值；
的解集为P，且
，求实数a的取值范围；
的值及曲线
处的切线方程；
的单调区间。推荐套卷
（本小题满分10分）选修4-1：几何证明选讲
已知AB是⊙O的直径，F为圆上一点，∠BAF的角平分线与圆交于点C过点C作圆的切线与直线相交于点D，若AB＝6，∠DAB＝
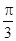
（1）证明：AD⊥CD；
（2）求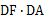的值及四边形ABCD的面积．
粤公网安备 44130202000953号