一辆客车从甲地出发前往乙地，平均速度
（千米/小时）与所用时间
（小时）的函数关系如图所示，其中
．
（1）直接写出与的函数关系式；
（2）若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶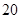
千米，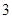
小时后两车相遇．
①求两车的平均速度；
②甲、乙两地间有两个加油站
、
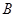，它们相距
千米，当客车进入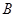加油站时，货车恰好进入加油站（两车加油的时间忽略不计），求甲地与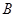加油站的距离．
是不共面的直线，且
，
，
，求证：
．
，点A∈直线b。A∈
，
，
，求证：
。
、
、
两两异面，空间与
推荐套卷
一辆客车从甲地出发前往乙地，平均速度（千米/小时）与所用时间（小时）的函数关系如图所示，其中．
（1）直接写出与的函数关系式；
（2）若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶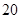千米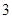，小时后两车相遇．
①求两车的平均速度；
②甲、乙两地间有两个加油站、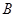，它们相距千米，当客车进入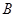加油站时，货车恰好进入加油站（两车加油的时间忽略不计），求甲地与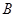加油站的距离．
粤公网安备 44130202000953号