某校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．
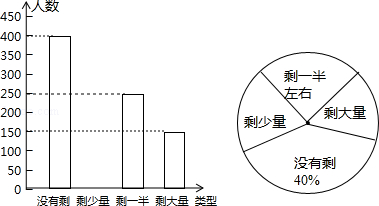
（1）这次被调查的同学共有 名；
（2）把条形统计图补充完整；
（3）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校18 000名学生一餐浪费的食物可供多少人食用一餐？
相关试题
是方程
的两实根，求
的值。
，使得函数
在闭区间
上的最大值是1？若存在，求出对应的（本小题满分12分）若函数
的图象与直线
相切，
并且相邻两个切点的距离为
．
（1）求
，
的值；
（2）将
的图象向右平移
个单位后，所得的图象
对应的函数
恰好是偶函数，求最
小正数，并求的单调递增区间。
,
，求
的值．
、
是关于
的二次方程
的两根，
，求
的范围。推荐套卷
粤公网安备 44130202000953号