如图,在平面直角坐标系中,抛物线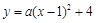 与
与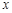 轴交于
轴交于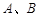 两点,与
两点,与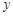 轴交于点
轴交于点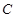 ,且点
,且点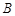 的坐标为
的坐标为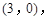 点
点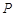 在这条抛物线上,且不与
在这条抛物线上,且不与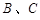 两点重合,过点
两点重合,过点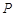 作
作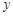 轴的垂线与射线
轴的垂线与射线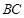 交于点
交于点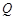 ,以
,以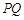 为边作
为边作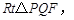 使
使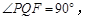 点
点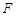 在点
在点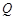 的下方,且
的下方,且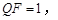 设线段
设线段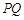 的长度为
的长度为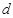 ,点
,点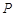 的横坐标为
的横坐标为 .
.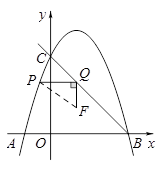
(1)求这条抛物线所对应的函数表达式;
(2)求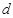 与
与 之间的函数关系式;
之间的函数关系式;
(3)当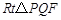 的边
的边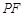 被
被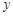 轴平分时,求
轴平分时,求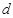 的值;
的值;
(4)以 为边作等腰直角三角形
为边作等腰直角三角形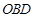 ,当
,当 时,直接写出点
时,直接写出点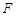 落在
落在 的边上时
的边上时 的值.
的值.
相关知识点
推荐套卷
如图,在平面直角坐标系中,抛物线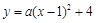 与
与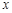 轴交于
轴交于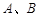 两点,与
两点,与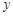 轴交于点
轴交于点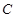 ,且点
,且点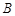 的坐标为
的坐标为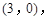 点
点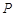 在这条抛物线上,且不与
在这条抛物线上,且不与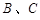 两点重合,过点
两点重合,过点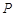 作
作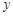 轴的垂线与射线
轴的垂线与射线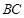 交于点
交于点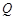 ,以
,以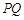 为边作
为边作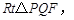 使
使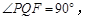 点
点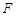 在点
在点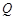 的下方,且
的下方,且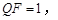 设线段
设线段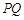 的长度为
的长度为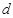 ,点
,点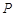 的横坐标为
的横坐标为 .
.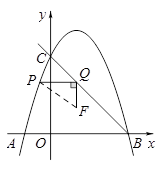
(1)求这条抛物线所对应的函数表达式;
(2)求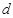 与
与 之间的函数关系式;
之间的函数关系式;
(3)当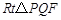 的边
的边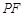 被
被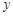 轴平分时,求
轴平分时,求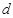 的值;
的值;
(4)以 为边作等腰直角三角形
为边作等腰直角三角形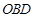 ,当
,当 时,直接写出点
时,直接写出点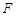 落在
落在 的边上时
的边上时 的值.
的值.