（本题10分）在“走基层,树新风”活动中，青年记者石剑深入边远山区，随机走访农户，调查农村儿童生活教育现状。根据收集的数据字编制了不完整的统计图表如下：
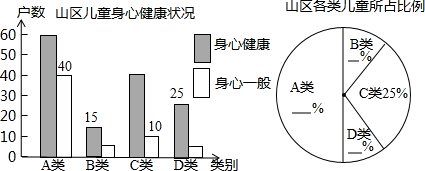
请你用学过的统计知识,解决问题：
（1）记者石剑走访了边远山区多少家农户?
（2）将统计图表中的空缺数据正确填写完整；
（3）分析数据后，请你提一条合理建议．
相关试题
( 本题8分) 已知函数
的图象经过点
(- 3, - 2)及点
(1, 6).(1) 求此一次函数解析式,并画图象;
(2) 求此函数图象与坐标轴围成的三角形的面积.
，其中x = -2,y = 
．
粤公网安备 44130202000953号