【2015高考陕西,文23】选修4-4:坐标系与参数方程
在直角坐标版权法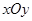 吕,直线
吕,直线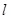 的参数方程为
的参数方程为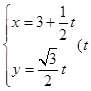 为参数),以原点为极点,
为参数),以原点为极点,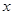 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系,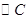 的极坐标方程为
的极坐标方程为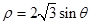 .
.
(Ⅰ)写出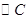 的直角坐标方程;
的直角坐标方程;
(Ⅱ)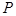 为直线
为直线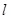 上一动点,当
上一动点,当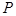 到圆心
到圆心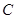 的距离最小时,求点
的距离最小时,求点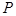 的坐标.
的坐标.
推荐套卷
【2015高考陕西,文23】选修4-4:坐标系与参数方程
在直角坐标版权法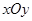 吕,直线
吕,直线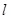 的参数方程为
的参数方程为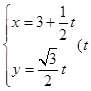 为参数),以原点为极点,
为参数),以原点为极点,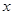 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系,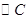 的极坐标方程为
的极坐标方程为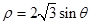 .
.
(Ⅰ)写出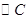 的直角坐标方程;
的直角坐标方程;
(Ⅱ)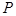 为直线
为直线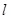 上一动点,当
上一动点,当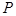 到圆心
到圆心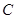 的距离最小时,求点
的距离最小时,求点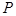 的坐标.
的坐标.