已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．
当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；
当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．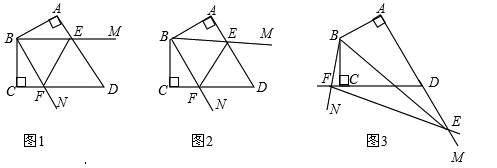
相关知识点
推荐套卷
已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．
当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；
当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．
粤公网安备 44130202000953号