莘县旅游资源丰富,其中燕塔是莘县著名旅游景点(如图①).一天身高1.5m的小明从A处仰视观看燕塔顶部,其仰角为30°.小明又向西走了30m,∠APB=15°(如图②).请你帮小明算出雁塔的高度.(结果保留一位小数,参考数据: ≈1.41,
≈1.41,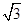 ≈1.73)
≈1.73)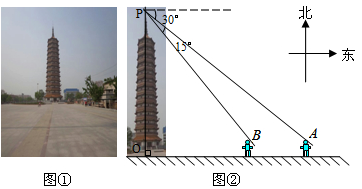
相关知识点
推荐套卷
莘县旅游资源丰富,其中燕塔是莘县著名旅游景点(如图①).一天身高1.5m的小明从A处仰视观看燕塔顶部,其仰角为30°.小明又向西走了30m,∠APB=15°(如图②).请你帮小明算出雁塔的高度.(结果保留一位小数,参考数据: ≈1.41,
≈1.41,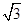 ≈1.73)
≈1.73)