（本小题满分10分）选修4-4：坐标系与参数方程
将圆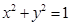
上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C．
（Ⅰ）写出C的参数方程；
（Ⅱ）设直线
与C的交点为
，以坐标原点为极点，x轴正半轴为极坐标建立极坐标系，求过线段
的中点且与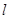
垂直的直线的极坐标方程．
，过P作直线
与圆相交于A、B，求弦AB中点的轨迹方程。
，求过点（1，
）的切线方程
，求过点P（3，1）圆的切线方程。
轴所得弦长为
；②被
轴分成两段圆弧，其弧长的比为
；③圆心到直线
：
的距离为
的圆的方程。
与已知圆
的交点，且在两坐标轴上的四个截距之和为8的圆的方程。
的单调性，并求其值域。相关知识点
推荐套卷
（本小题满分10分）选修4-4：坐标系与参数方程
将圆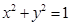上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C．
（Ⅰ）写出C的参数方程；
（Ⅱ）设直线与C的交点为，以坐标原点为极点，x轴正半轴为极坐标建立极坐标系，求过线段的中点且与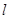垂直的直线的极坐标方程．
粤公网安备 44130202000953号