已知抛物线y=ax2+bx+c的顶点为(1,0),与y轴的交点坐标为(0, ).R(1,1)是抛物线对称轴l上的一点.
).R(1,1)是抛物线对称轴l上的一点.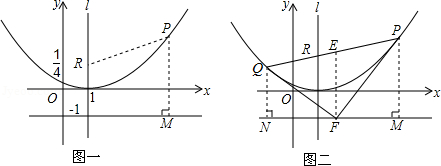
(1)求抛物线y=ax2+bx+c的解析式;
(2)若P是抛物线上的一个动点(如图一),求证:点P到R的距离与点P到直线y=﹣1的距离恒相等;
(3)设直线PR与抛物线的另一交点为Q,E为线段PQ的中点,过点P、E、Q分别作直线y=﹣1的垂线.垂足分别为M、F、N(如图二).求证:PF⊥QF.
相关知识点
推荐套卷
已知抛物线y=ax2+bx+c的顶点为(1,0),与y轴的交点坐标为(0, ).R(1,1)是抛物线对称轴l上的一点.
).R(1,1)是抛物线对称轴l上的一点.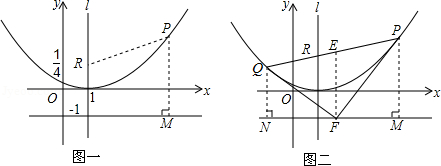
(1)求抛物线y=ax2+bx+c的解析式;
(2)若P是抛物线上的一个动点(如图一),求证:点P到R的距离与点P到直线y=﹣1的距离恒相等;
(3)设直线PR与抛物线的另一交点为Q,E为线段PQ的中点,过点P、E、Q分别作直线y=﹣1的垂线.垂足分别为M、F、N(如图二).求证:PF⊥QF.