一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P (x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.
相关知识点
推荐套卷

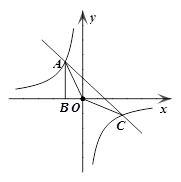
 沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO=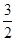 .
.
 y.
y.
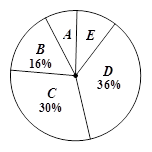
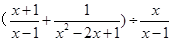 ,其中负数x的值是方程x2-2=0的解.
,其中负数x的值是方程x2-2=0的解. 粤公网安备 44130202000953号
粤公网安备 44130202000953号