(本小题满分8分)按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:

(a)新数据都在60~100(含60和100)之间;
(b)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y与x的关系是y=x+p(100-x),请说明:当p=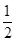 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
(2)若按关系式y=a(x-h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)