如图，在水平地面上竖立着一面墙AB，墙外有一盏路灯D．光线DC恰好通过墙的最高点B，且与地面形成37°角．墙在灯光下的影子为线段AC，并测得AC=5．5米．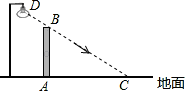
（1）求墙AB的高度（结果精确到0．1米）；（参考数据：tan37°≈0．75，sin37°≈0．60，cos37°≈0．80）
（2）如果要缩短影子AC的长度，同时不能改变墙的高度和位置，请你写出两种不同的方法．
，其中
．
，先化简
，再求它的值；
的两根，求
．
，其中
=2．
，其中
，
．
－2cos45°+
．相关知识点
推荐套卷
如图，在水平地面上竖立着一面墙AB，墙外有一盏路灯D．光线DC恰好通过墙的最高点B，且与地面形成37°角．墙在灯光下的影子为线段AC，并测得AC=5．5米．
（1）求墙AB的高度（结果精确到0．1米）；（参考数据：tan37°≈0．75，sin37°≈0．60，cos37°≈0．80）
（2）如果要缩短影子AC的长度，同时不能改变墙的高度和位置，请你写出两种不同的方法．
粤公网安备 44130202000953号