(本小题5分)我们定义:如图1,矩形MNPQ中,点K、O、G、H分别在NP、PQ、QM、MN上,若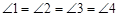 ,则称四边形KOGH为矩形MNPQ的反射四边形.如图2、图3四边形ABCD、A’B’C’D’均为矩形,它们都是由32个边长为1的正方形组成的图形,点E、F、E’、F’分别在BC、CD、B’C’、C’D’边上,试利用正方形网格在图2、图3中分别画出矩形ABCD和矩形A’B’C’D’的反射四边形EFGH和E’F’G’H’.
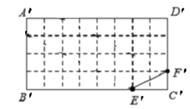
,则称四边形KOGH为矩形MNPQ的反射四边形.如图2、图3四边形ABCD、A’B’C’D’均为矩形,它们都是由32个边长为1的正方形组成的图形,点E、F、E’、F’分别在BC、CD、B’C’、C’D’边上,试利用正方形网格在图2、图3中分别画出矩形ABCD和矩形A’B’C’D’的反射四边形EFGH和E’F’G’H’.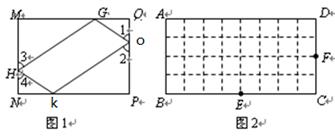
相关知识点
推荐套卷
(本小题5分)我们定义:如图1,矩形MNPQ中,点K、O、G、H分别在NP、PQ、QM、MN上,若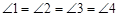 ,则称四边形KOGH为矩形MNPQ的反射四边形.如图2、图3四边形ABCD、A’B’C’D’均为矩形,它们都是由32个边长为1的正方形组成的图形,点E、F、E’、F’分别在BC、CD、B’C’、C’D’边上,试利用正方形网格在图2、图3中分别画出矩形ABCD和矩形A’B’C’D’的反射四边形EFGH和E’F’G’H’.
,则称四边形KOGH为矩形MNPQ的反射四边形.如图2、图3四边形ABCD、A’B’C’D’均为矩形,它们都是由32个边长为1的正方形组成的图形,点E、F、E’、F’分别在BC、CD、B’C’、C’D’边上,试利用正方形网格在图2、图3中分别画出矩形ABCD和矩形A’B’C’D’的反射四边形EFGH和E’F’G’H’.
